Summary
$$\displaylines{\begin{align}\sin^2x+\cos^2x&=1\\1+\cot^2x&=\csc^2x\\\tan^2x+1&=\sec^2x\\\sin(a\pm b)&=\sin a\cos b\pm\sin b\cos a\\\cos(a\pm b)&=\cos a\cos b\mp\sin a\sin b\\\tan(a\pm b)&=\frac{\tan a\pm\tan b}{1\mp\tan a\tan b}\\\sin(2x)&=2\sin x\cos x\\\cos(2x)&=\cos^2x-\sin^2x\\\cos(2x)&=2\cos^2x-1\\\cos(2x)&=1-2\sin^2x\\\tan(2x)&=\frac2{\cot x-\tan x}\\\cos\frac x2&=\pm\sqrt\frac{1+\cos x}2\\\sin\frac x2&=\pm\sqrt\frac{1-\cos x}2\\\tan\frac x2&=\pm\sqrt\frac{1-\cos x}{1+\cos x}\\\tan\frac x2&=\frac{\sin x}{1+\cos x}\\\tan \frac x2&=\frac{1-\cos x}{\sin x}\end{align}}$$
Each of those will be discussed below.
Pythagorean Identities
$$\sin^2x+\cos^2x=1$$
Very elegant formula. Think about it in the context of the unit circle where $x^2+y^2=1$.
From this identity, two more came:
$$\displaylines{1+\cot^2x=\csc^2x\\\tan^2x+1=\sec^2x}$$
Proof:
Divide both sides of the first identity by $\sin^2x$ and $\cos^2x$, respectively.
Angle Sum/Difference
$$\displaylines{\sin(a\pm b)=\sin a\cos b\pm\sin b\cos a\\\cos(a\pm b)=\cos a\cos b\mp\sin a\sin b}$$
Proof:
This image from Wikipedia should be self-explanatory.
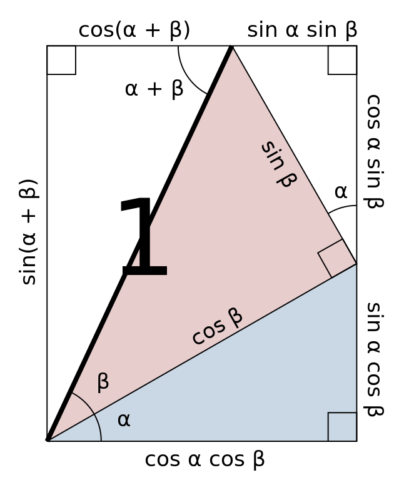
$$\tan(a\pm b)=\frac{\tan a\pm\tan b}{1\mp\tan a\tan b}$$
Proof:
$$\displaylines{\begin{align}\tan(a\pm b)&=\frac{\sin(a\pm b)}{\cos(a\pm b)}\\&=\frac{(\sin a\cos b\pm\sin b\cos a)(\frac1{\cos a\cos b})}{(\cos a\cos b\mp\sin a\sin b)(\frac1{\cos a\cos b})}\\&=\frac{\frac{\sin a}{\cos a}\pm\frac{\sin b}{\cos b}}{1\mp\frac{\sin a\sin b}{\cos a\cos b}}\\&=\frac{\tan a\pm\tan b}{1\mp\tan a\tan b}\end{align}}$$
Double Angle
$$\displaylines{\begin{align}\sin(2x)&=2\sin x\cos x\\\cos(2x)&=\cos^2x-\sin^2x\\\tan(2x)&=\frac2{\cot x-\tan x}\end{align}}$$
Proof:
Expand the Angle Sum formulae above for $a=x$ and $b=x$ to get this formula.
$$\cos(2x)=2\cos^2x-1=1-2\sin^2x$$
Proof:
Use the Pythagorean Identity and the cosine Double Angle identity above.
Half Angle
$$\displaylines{\cos\frac x2=\pm\sqrt\frac{1+\cos x}2\\\sin\frac x2=\pm\sqrt\frac{1-\cos x}2}$$
Where the sign before the square root varies based on the value of $x$ (you should be able to figure that out!).
Proof:
$$\displaylines{\cos(2x)=2\cos^2x-1\\\cos x=2\cos^2\frac x2-1\\1+\cos x=2\cos^2\frac x2\\\frac{1+\cos x}2=\cos^2\frac x2\\\cos\frac x2=\pm\sqrt\frac{1+\cos x}2}$$
And
$$\displaylines{\cos(2x)=1-2\sin^2x\\\cos x=1-2\sin^2\frac x2\\1-\cos x=2\sin^2\frac x2\\\frac{1-\cos x}2=\sin^2\frac x2\\\sin\frac x2=\pm\sqrt\frac{1-\cos x}2}$$
$$\tan\frac x2=\pm\sqrt\frac{1-\cos x}{1+\cos x}$$
Proof:
Should be straightforward given the above two Half Angle identities and that $\tan x=\frac{\sin x}{\cos x}$.
$$\tan\frac x2=\frac{\sin x}{1+\cos x}=\frac{1-\cos x}{\sin x}$$
Proof:
Multiply both the numerator and the denominator of the previous tangent Half Angle identity by $1+\cos x$ and $1-\cos x$, respectively, and use the Pythagorean identities.
References
Wikipedia, List of trigonometric identities, https://en.wikipedia.org/wiki/List_of_trigonometric_identities
Wikipedia, Proofs of trigonometric identities, https://en.wikipedia.org/wiki/Proofs_of_trigonometric_identities