Question:
Please find an equation of the following sinusoid, in the form $a\sin{bx+c}$: $$2\cos{2x}-7\sin{2x}$$
Just face it, although it is certainly quite possible to find a sinusoid by pure math (shown at the bottom of this post), we all would like a shortcut to it. And here is the shortcut…
This method can be used to find equations of sinusoids where the coefficient before $X$ is the same only.
1. Graph the function.
Take out your TI-84+ CE and type the equation in $Y_1$, like this:
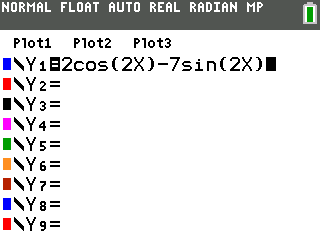
Step-by-step: [y=] [clear] <type in equation>
2. Get the data points.
Then, we need to pick out a set of data points for the next step to find our sinusoid. To do this, we need a sequence (list) of $x$ values, store them in $L_1$, a sequence of $y$ values, and store them in $L_2$.
For the list of $x$ values, we can choose, really, any series of numbers. For example, we can choose a sequence like $\{0,0.1,0.2,0.3,…,4\}$. This series can be generated with the $\operatorname{seq}($ function. It is located in [2nd] [stat] [right arrow]:
After you enter, you will be greeted with this wizard.
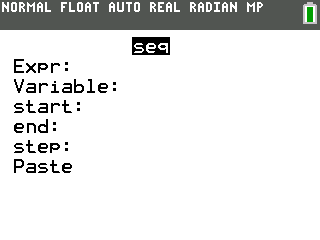
Fill the wizard with these values, which will generate a list from $0$ to $4$, with $0.1$ between each two numbers:
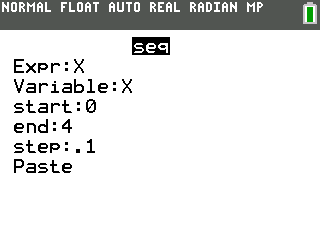
Then, you can Paste the command and store it to the list $L_1$, like this:
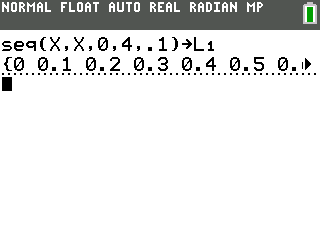
Step-by-step: [2nd] [stat] [right arrow] [5] <fill in the values as shown> <Paste> [sto->] [2nd] [1] [enter]
(To learn more about the $\operatorname{seq}($ function, please check this post)
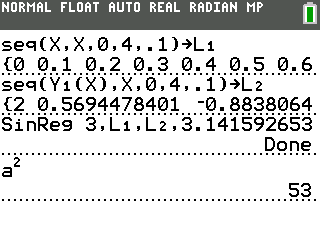
Now we need to find the $y$ values. To generate the $y$ values, we need to find the value of $Y_1(x)$ for each $X$ that we chose, where $Y_1$ is the equation you typed in Step 1. This can be done with the command $\operatorname{seq}(Y_1(X),X,0,4,.1)\rightarrow L_2$.
(The $Y_1$ token can be found in [vars] [right arrow] [enter].)
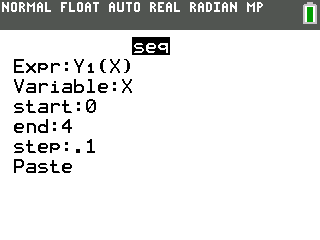
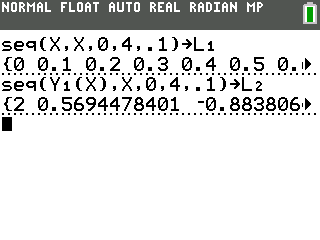
Step-by-step: [2nd] [stat] [right arrow] [5] <fill in the values as shown> <Paste> [sto->] [2nd] [2] [enter]
This command will take a pretty long time to load, so be patient!
Now we have our points in the lists, we can start finding the sinusoid equation!
3. Find the equation.
To finally find our sinusoid, we will use the $SinReg$ function on the calculator. It is located in [stat] [right arrow].
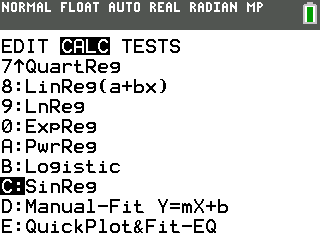
Select this token and press [enter]. You will be greeted with this other wizard:
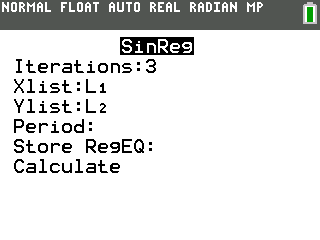
In here, you don’t need to worry about Iterations, Xlist, or Ylist, since they are prefilled for you. You however need to type in the Period, which as you should know is equal to $2\pi/b$, which in our case is $2\pi/2=\pi$.
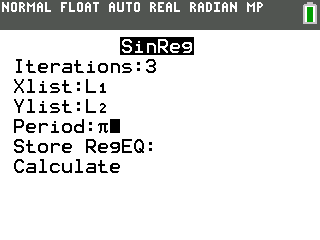
You do not need to type in a value for Store RegEQ. After you fill in the values, just press Calculate and wait for a looooong time.
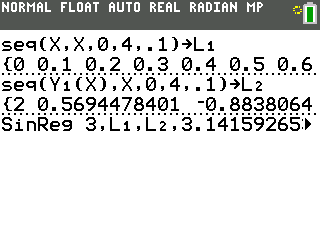
After the command is finished, the final answer will be displayed on the screen:

(Note: The number $d$ above has the value $-8.497336384\text{E}-15$. This is an extremely small number, so we do not need to consider it in the final answer.)
And congratulations, you just had your calculator solve your problem! The unsimplified final answer is:
$7.280109889\sin{(2x+2.863292995)}$
4. Finalize your answers.
However, usually, you don’t want to write this huge decimal $7.280109889$ on your answer sheet. Fortunately, this value $a$ is usually a square root of some number (which you should know if you have done this kind of problem by hand), so we can take the square of that. The number $a$ can be found in [vars] [5] [right arrow] [right arrow]:
After we take the square, we find that the number $a$ is the square root of $53$.
If you have solved these problems by hand, you would also know that $c$ should be in the form $\arcsin{\frac{\theta}a}$. So we can further simplify the answer with these steps:
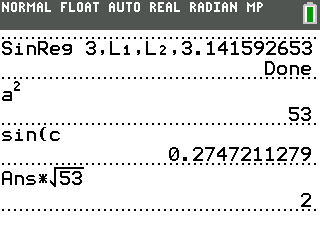
These calculations show that $c$ is $\arcsin{\frac{2}{\sqrt{53}}}$.
So, our final, simplified answer would be:
$$y=\boxed{\sqrt{53}\sin{(2x+\arcsin{\frac{2}{\sqrt{53}}})}}$$
Conclusion
We have found an equation for a sinusoid with a TI-84+CE calculator. However, this does not mean that you don’t have to learn how to do it on your own! You should still know the algebra way of solving these questions.
Appendix. The algebra way.
$$2\cos{2x}-7\sin{2x}\text{, write as }a\sin(bx+c)$$ $$\displaylines{ \begin{align} a\sin{(bx+c)}&=a(\sin{bx}\cos{c}+\cos{bx}\sin{c}) \\ &=(a\cos{c})\sin{bx}+(a\sin{c})\cos{bx} \end{align} }$$ $$\displaylines{ b=2\text{, }a\cos{c}=-7\text{, }a\sin{c}=2 \\ \begin{align} (a\cos{c})^2+(a\sin{c})^2&=(-7)^2+2^2 \\ a^2\cos^2{c}+a^2\sin^2{c}&=49+4 \\ a^2(\cos^2{c}+\sin^2{c})&=53 \\ a^2&=53 \\ a&=\pm\sqrt{53} \end{align} }$$ $$\displaylines{ \begin{align} \sqrt{53}\sin{c}&=2 \\ \sin{c}&=\frac{2}{\sqrt{53}} \\ c&=\arcsin\frac{2}{\sqrt{53}} \end{align} }$$ $$\displaylines{ \begin{align} 2\cos{2x}-7\sin{2x}&=a\sin(bx+c) \\ &=\boxed{\sqrt{53}\sin(2x+\arcsin\frac{2}{\sqrt{53}})} \end{align} }$$